| ГОСТ 2.317-69 МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ ЕДИНАЯ СИСТЕМА КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ ИПК
ИЗДАТЕЛЬСТВО СТАНДАРТОВ МЕЖГОСУДАРСТВЕННЫЙ СТАНДАРТ
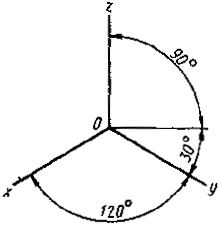
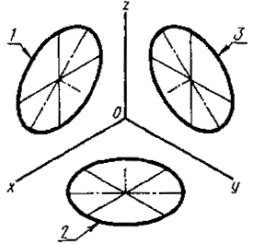
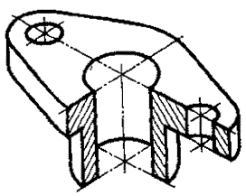
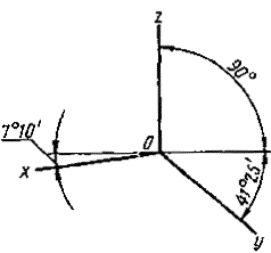
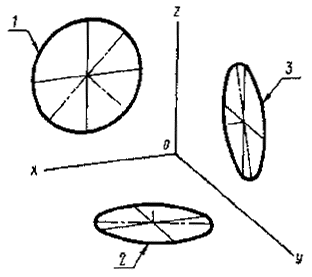
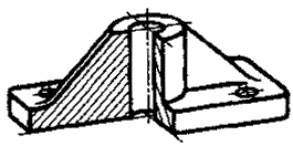
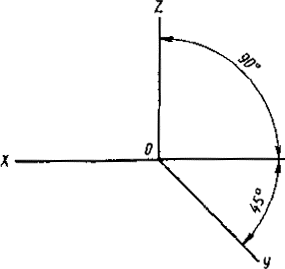
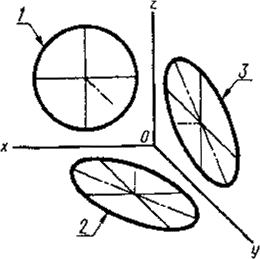
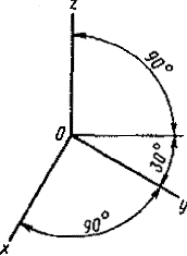
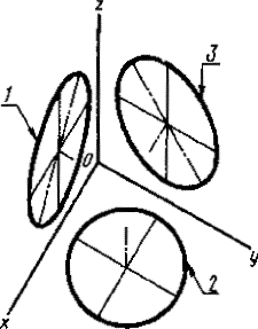
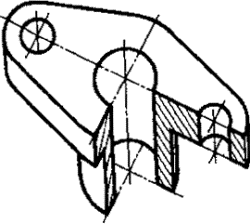
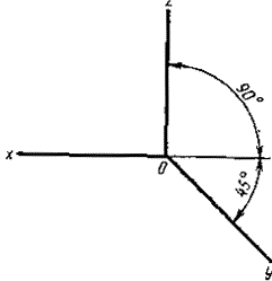
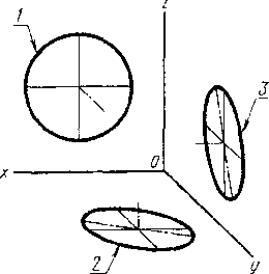
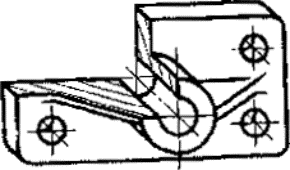
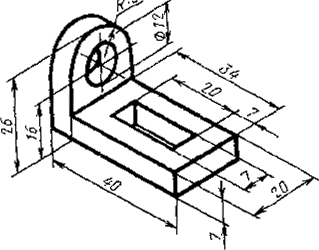
Постановлением Комитета стандартов, мер и измерительных приборов при Совете Министров СССР от 14 октября 1969 г. № 1118 срок введения установлен с 01.01.71 Настоящий стандарт устанавливает аксонометрические проекции, применяемые в чертежах всех отраслей промышленности и строительства. Стандарт полностью соответствует СТ СЭВ 1979-79. (Измененная редакция, Изм. № 1). 1. ПРЯМОУГОЛЬНЫЕ ПРОЕКЦИИ1.1. Изометрическая проекция 1.1.1. Положение аксонометрических осей приведено на черт. 1. 1.1.2. Коэффициент искажения по осям х, у, z равен 0,82. Изометрическую проекцию для упрощения, как правило, выполняют без искажения по осям х, у, z, т. е. приняв коэффициент искажения равным 1. 1.1.3. Окружности, лежащие в плоскостях, параллельных плоскостям проекций проецируются на аксонометрическую плоскость проекций в эллипсы (черт. 2). Если изометрическую проекцию выполняют без искажения по осям х, у, z, то большая ось эллипсов 1, 2, 3 равна 1,22, а малая ось - 0,71 диаметра окружности. Если изометрическую проекцию выполняют с искажением по осям х, у, z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось - 0,58 диаметра окружности. 1.1.4. Пример изометрической проекции детали приведен на черт. 3. 1.2. Диметрическая проекция 1.2.1. Положение аксонометрических осей приведено на черт. 4. 1.2.2. Коэффициент искажения по оси у равен 0,47, а по осям х и z - 0,94. Диметрическую проекцию, как правило, выполняют без искажения по осям х и z и с коэффициентом искажения 0,5 по оси у. Черт. 1 1 - эллипс (большая ось расположена под углом 90° к оси у); 2 - эллипс (большая ось расположена под углом 90° к оси z); 3 - эллипс (большая ось расположена под углом 90° к оси х). Черт. 2 Черт. 3 1.2.3. Окружности, лежащие в плоскостях, параллельных плоскостям проекций, проецируются на аксонометрическую плоскость проекций в эллипсы (черт. 5). Если диметрическую проекцию выполняют без искажения по осям х и z, то большая ось эллипсов 1, 2, 3 равна 1,06 диаметра окружности, а малая ось эллипса 1 - 0,95, эллипсов 2 и 3 - 0,35 диаметра окружности. Если диметрическую проекцию выполняют с искажением по осям х и z, то большая ось эллипсов 1, 2, 3 равна диаметру окружности, а малая ось эллипса 1 - 0,9, эллипсов 2 и 3 - 0,33 диаметра окружности. 1.2.4. Пример диметрической проекции детали приведен на черт. 6. Черт. 4 1 - эллипс (большая ось
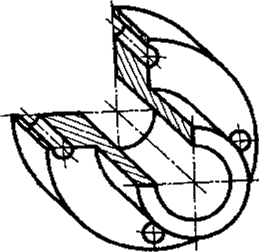
расположена под углом 90° к оси у); Черт. 5 Черт. 6 2. КОСОУГОЛЬНЫЕ ПРОЕКЦИИ2.1. Фронтальная изометрическая проекция 2.1.1. Положение аксонометрических осей приведено на черт. 7. Допускается применять фронтальные изометрические проекции с углом наклона оси у 30 и 60°. 2.1.2. Фронтальную изометрическую проекцию выполняют без искажения по осям х, у, z. 2.1.3. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, - в эллипсы (черт. 8). Большая ось эллипсов 2 и 3 равна 1,3, а малая ось - 0,54 диаметра окружности. 2.1.4. Пример фронтальной изометрической проекции детали приведен на черт. 9. Черт. 7 1 - окружность; Черт. 8 Черт. 9 2.2. Горизонтальная изометрическая проекция 2.2.1. Положение аксонометрических осей приведено на черт. 10. Допускается применять горизонтальные изометрические проекции с углом наклона оси у 45 и 60°, сохраняя угол между осями х и у 90°. 2.2.2. Горизонтальную изометрическую проекцию выполняют без искажения по осям х, у и z. 2.2.3. Окружности, лежащие в плоскостях, параллельных горизонтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных фронтальной и профильной плоскостям проекций - в эллипсы (черт. 11). Большая ось эллипса 1 равна 1,37, а малая ось - 0,37 диаметра окружности. Большая ось эллипса 3 равна 1,22, а малая ось - 0,71 диаметра окружности. 2.2.4. Пример горизонтальной изометрической проекции приведен на черт. 12. Черт. 10 1 - эллипс (большая ось
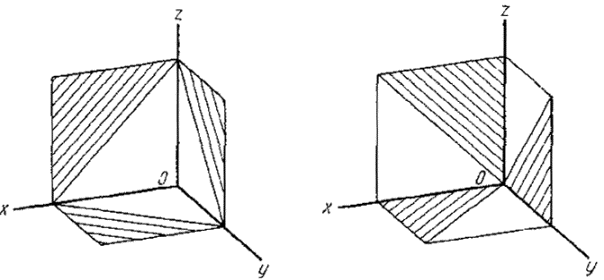
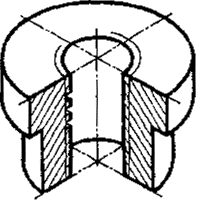
составляет с осью z угол 15°); Черт. 11 Черт. 12 2.3. Фронтальная диметрическая проекция 2.3.1. Положение аксонометрических осей приведено на черт. 13. Допускается применять фронтальные диметрические проекции с углом наклона оси у 30 и 60°. Коэффициент искажения по оси у равен 0,5, а по осям х и z - 1. 2.3.2. Окружности, лежащие в плоскостях, параллельных фронтальной плоскости проекций, проецируются на аксонометрическую плоскость проекций в окружности, а окружности, лежащие в плоскостях, параллельных горизонтальной и профильной плоскостям проекций, - в эллипсы (черт. 14). Большая ось эллипсов 2 и 3 равна 1,07, а малая ось - 0,33 диаметра окружности. 2.3.3. Пример фронтальной диметрической проекции детали приведен на черт. 15. Черт. 13 1 - окружность; Черт. 14 Черт. 15 3. УСЛОВНОСТИ И НАНЕСЕНИЕ РАЗМЕРОВ 3.1. Линии штриховки сечений в аксонометрических проекциях наносят параллельно одной из диагоналей проекций квадратов, лежащих в соответствующих координатных плоскостях, стороны которых параллельны аксонометрическим осям (черт. 16). Черт. 16 3.2. При нанесении размеров выносные линии проводят параллельно аксонометрическим осям, размерные линии - параллельно измеряемому отрезку (черт. 17). 3.3. В аксонометрических проекциях спицы маховиков и шкивов, ребра жесткости и подобные элементы штрихуют (см. черт. 6). 3.4. При выполнении в аксонометрических проекциях зубчатых колес, реек, червяков и подобных элементов допускается применять условности по ГОСТ 2.402-68. В аксонометрических проекциях резьбу изображают по ГОСТ 2.311-68. Допускается изображать профиль резьбы полностью или частично, как показано на черт. 18. Черт. 17 Черт. 18 3.5. В необходимых случаях допускается применять другие теоретически обоснованные аксонометрические проекции. |