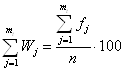"ГОСТ 23615-79* (СТ СЭВ 5061-85). Система обеспечения точности геометрических параметров в строительстве. Статистический анализ точности" // Технорма.RU

Введен в действие

Постановлением Госстроя СССР

от 12 апреля 1979 г. N 55

ГОСУДАРСТВЕННЫЙ СТАНДАРТ СОЮЗА ССР

СИСТЕМА ОБЕСПЕЧЕНИЯ ТОЧНОСТИ ГЕОМЕТРИЧЕСКИХ

ПАРАМЕТРОВ В СТРОИТЕЛЬСТВЕ

СТАТИСТИЧЕСКИЙ АНАЛИЗ ТОЧНОСТИ

System for ensuring accuracy of geometrical

parameters in construction.

Statistical analysis of accuracy

ГОСТ 23615-79*

(СТ СЭВ 5061-85)

Группа Ж02

Срок введения

с 1 января 1980 года

Переиздание (май 1988 г.) с Изменением N 1, утвержденным в июне 1986 г. (ИУС-11-86).

Настоящий стандарт устанавливает общие правила статистического анализа точности геометрических параметров при изготовлении строительных элементов (деталей, изделий, конструкций), выполнении разбивочных работ в процессе строительства и установке элементов в конструкциях зданий и сооружений.

Стандарт распространяется на технологические процессы и операции массового и серийного производства.

Применяемые в стандарте термины по статистическому анализу и контролю соответствуют приведенным в ГОСТ 15895-77.

Стандарт полностью соответствует СТ СЭВ 5061-85.

(Измененная редакция, Изм. N 1).

1. ОБЩИЕ ПОЛОЖЕНИЯ

1.1. Статистическим анализом устанавливают закономерность распределения действительных значений геометрических параметров конструкций зданий и сооружений и их элементов и определяют статистические характеристики точности этих параметров.

1.2. На основе результатов статистического анализа:

производят оценку действительной точности и устанавливают возможности технологических процессов и операций по ее обеспечению;

определяют возможность применения статистических методов регулирования точности по СТ СЭВ 2835-80 и контроля точности по ГОСТ 23616-79;

проверяют эффективность применяемых методов регулирования и контроля точности при управлении технологическими процессами.

1.3. Статистический анализ точности выполняют отдельно по каждому геометрическому параметру в следующей последовательности:

в зависимости от характера производства образуют необходимые выборки и определяют действительные отклонения параметра от номинального;

рассчитывают статистические характеристики действительной точности параметра в выборках;

проверяют статистическую однородность процесса - согласие опытного распределения действительных отклонений параметра с теоретическим и стабильность статистических характеристик в выборках;

оценивают точность технологического процесса и, в зависимости от цели анализа, принимают решение о порядке применения его результатов.

1.4. Статистический анализ точности следует проводить после предварительного изучения состояния технологического процесса в соответствии с требованиями СТ СЭВ 2835-80 и его наладки по полученным результатам.

1.5. Действительные отклонения геометрического параметра в выборках определяют в результате его измерений в соответствии с требованиями ГОСТ 23616-79 и ГОСТ 26433.0-85.

1.2 - 1.5. (Измененная редакция, Изм. N 1).

2. ОБРАЗОВАНИЕ ВЫБОРОК

2.1. В качестве исследуемой генеральной совокупности принимают объем продукции или работ (например разбивочных), производимый на технологической линии (потоке, участке и т.п.) при неизменных типовых условиях производства в течение определенного времени, достаточного для характеристики данного процесса.

2.2. Статистический анализ точности выполняют по действительным отклонениям параметра в представительной объединенной выборке, состоящей из не менее чем 100 объектов контроля и получаемой путем последовательного отбора из исследуемой совокупности серии выборок малого объема.

Эти выборки отбирают через равные промежутки времени, определяемые в зависимости от объема производства и особенностей технологического процесса.

(Измененная редакция, Изм. N 1).

2.3. При анализе точности процессов изготовления элементов массового производства, когда на каждой единице или комплекте технологического оборудования постоянно в достаточно большом объеме производится однотипная продукция (например кирпич, асбестоцементные листы), отбирают серию мгновенных выборок одинакового объема единицам.

2.4. При анализе точности изготовления элементов серийного производства, когда достаточный объем продукции может быть получен с нескольких однотипных единиц технологического оборудования (например производство ряда видов железобетонных изделий, сборка металлоконструкций и т.п.), отбирают серию выборок одинакового объема единицам. Эти выборки могут быть составлены из изделий, отбираемых при приемочном контроле нескольких последовательных или параллельных партий продукции.

2.5. При анализе точности разбивки осей и установки элементов образуют серию выборок одинакового объема из закрепленных в натуре ориентиров или элементов, установленных на одном или нескольких монтажных горизонтах.

2.4, 2.5 (Измененная редакция, Изм. N 1).

2.6. Порядок формирования выборки для обеспечения ее представительности и случайности определяют в соответствии с характером объекта исследований и требованиями ГОСТ 18321-73.

3. РАСЧЕТ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ТОЧНОСТИ

3.1. При проведении статистического анализа вычисляют выборочные средние отклонения, а также выборочные средние квадратические отклонения или размахи действительных отклонений в выборках.

Примечание. При анализе точности конфигурации элементов выборочные средние отклонения не вычисляют.

3.2. Выборочное среднее отклонение в выборках малого объема и в объединенной выборке вычисляют по формуле

, (1)

где - действительное отклонение;

- объем выборки.

3.3. Выборочное среднее квадратическое отклонение в выборках малого объема единицам и в объединенной выборке вычисляют по формуле

. (2)

В случаях, когда выборочное среднее отклонение в соответствии с примечанием к п. 3.1 не вычисляют, значение в формуле (2) принимают равным нулю.

3.4. Размахи действительных отклонений параметра определяют в выборках малого объема из единицам по формуле

, (3)

где и - наибольшие и наименьшие значения в выборке.

3.1 - 3.4 (Измененная редакция, Изм. N 1).

3.5. Порядок расчета статистических характеристик приведен в рекомендуемом Приложении 1.

3.6. В качестве статистических характеристик точности процесса принимают значения и в объединенной выборке, если результаты проведенной в соответствии с разд. 4 проверки подтвердили статистическую однородность процесса.

Значения , и в выборках малого объема используют при проверке однородности процесса.

(Измененная редакция, Изм. N 1).

4. ПРОВЕРКА СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ ПРОЦЕССА

4.1. При проверке статистической однородности процесса устанавливают:

согласие распределения действительных отклонений параметра в объединенной выборке с теоретическим;

стабильность выборочного среднего отклонения , значение которого характеризует систематические погрешности процесса;

стабильность выборочного среднего квадратического отклонения или размаха , значения которых характеризуют случайные погрешности прогресса.

4.2. Согласие распределения действительных отклонений параметра с теоретическим устанавливают по ГОСТ 11.006-74.

Допускается использование других методов, принятых в математической статистике (например построение ряда отклонений на вероятностной бумаге и т.д.).

4.3. При нормальном распределении геометрического параметра стабильность статистических характеристик в мгновенных выборках и выборках малого объема единицам проверяют по попаданию их значений в доверительные интервалы, границы которых вычисляют для доверительной вероятности не менее 0,95.

В случае, если гипотеза о нормальном распределении геометрического параметра не может быть принята, применяют другие методы математической статистики.

4.1 - 4.3 (Измененная редакция, Изм. N 1).

4.4. (Исключен, Изм. N 1).

4.5. Проверку статистической однородности технологических процессов изготовления строительных элементов, а также геометрических параметров зданий и сооружений допускается выполнять упрощенным способом в соответствии с рекомендуемым Приложением 1.

Пример проверки приведен в справочном Приложении 2.

(Измененная редакция, Изм. N 1).

4.6. Процесс считается статистически однородным по данному геометрическому параметру, если распределение действительных отклонений в объединенной выборке приближается к нормальному и характеристики точности в серии выборок, составивших объединенную выборку, стабильны во времени.

4.7. В случае, если распределение действительных отклонений не соответствует нормальному, а характеристики точности в серии выборок малого объема не стабильны, процесс не может считаться налаженным и установившимся. В этом случае следует ввести операционный контроль, установить причины нестабильности точности и произвести соответствующую настройку оборудования, после чего повторить анализ.

В любом случае систематическая погрешность по абсолютной величине, превышающая значение 1,643 , должна быть устранена регулированием.

(Измененная редакция, Изм. N 1).

5. ОЦЕНКА ТОЧНОСТИ ПРОЦЕССА

5.1. На основании результатов статистического анализа устанавливают возможность процесса обеспечивать точность параметра в соответствии с определенным классом точности по ГОСТ 21779-82.

5.2. Класс точности определяют из условия

, (4)

где - ближайшее большее к значению значение допуска для данного интервала номинального размера в соответствующих таблицах ГОСТ 21779-82;

- коэффициент, принимаемый по таблице настоящего стандарта в зависимости от значения приемочного уровня дефектности , принятого при контроле точности по ГОСТ 23616-79.

────────┬─────────────┬──────────────┬──────────────┬─────────────

AQL, % │ 0,25 │ 1,5 │ 4,0 │ 10,0

────────┼─────────────┼──────────────┼──────────────┼─────────────

t │ 3,0 │ 2,4 │ 2,1 │ 1,6

5.3. Для сопоставления уровня точности различных производств или в различные промежутки времени следует использовать показатель уровня точности , характеризующий запас точности по отношению к допуску и определяемый по формуле

, (5)

где - выборочное среднее квадратическое отклонение, определяемое для статистически однородного процесса в случайных выборках объемом не менее 30 единиц.

5.1 - 5.3 (Измененная редакция, Изм. N1).

5.4. Если по абсолютному значению оказывается меньше чем 0,14, то следует считать, что запас точности отсутствует.

Если отрицательна и по своему абсолютному значению превышает 0,14, то это означает, что процесс перешел в более низкий класс точности.

При значении , приближающемся к 0,5, следует проверить возможность отнесения процесса к более высокому классу точности.

Приложение 1

Рекомендуемое

ПОРЯДОК РАСЧЕТА

СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК

И ПРОВЕРКИ СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ

ПРОЦЕССА УПРОЩЕННЫМ СПОСОБОМ

1. Действительные отклонения в выборках объемом единиц заносят в хронологическом порядке в табл. 1.

Характеристики и вычисляют по формулам (1) и (3) настоящего стандарта.

Таблица 1

Форма таблицы для расчета характеристик и

в мгновенных выборках объемом

─────────────────────────────────────────┬────┬────┬────┬────┬────

Дата измерений │ │ │ │ │

─────────────────────────────────────────┼────┼────┼────┼────┼────

Номер выборки │ 1 │ 2 │ 3 │... │...

────────────────────┬────────────────────┼────┼────┼────┼────┼────

│ i = 1 │ │ │ │ │

│ 2 │ │ │ │ │

дельта x │ 3 │ │ │ │ │

i │ 4 │ │ │ │ │

│ . │ │ │ │ │

│ n │ │ │ │ │

────────────────────┴────────────────────┼────┼────┼────┼────┼────

│ │ │ │ │

n │ │ │ │ │

SUM дельта x = │ │ │ │ │

i=1 i │ │ │ │ │

─────────────────────────────────────────┼────┼────┼────┼────┼────

n │ │ │ │ │

SUM дельта x │ │ │ │ │

i=1 i │ │ │ │ │

дельта x = ------------------- = │ │ │ │ │

m n │ │ │ │ │

│ │ │ │ │

─────────────────────────────────────────┼────┼────┼────┼────┼────

дельта x = │ │ │ │ │

i,max │ │ │ │ │

─────────────────────────────────────────┼────┼────┼────┼────┼────

дельта x = │ │ │ │ │

i,min │ │ │ │ │

─────────────────────────────────────────┼────┼────┼────┼────┼────

R = дельта x - дельта x = │ │ │ │ │

x i,max i,min │ │ │ │ │

2. Действительные отклонения в каждой из выборок объема единицам заносят в табл. 2.

Таблица 2

Форма таблицы для расчета характеристик и

в выборках объемом

────┬──────────────┬──────────────┬────────────┬──────────────────

N │ │ 2 │ │ 2

п/п │ дельта x │дельта x │дельта x + 1│ (дельта x + 1)

│ i │ i │ i │ i

────┼──────────────┼──────────────┼────────────┼──────────────────

1 │ │ │ │

2 │ │ │ │

3 │ │ │ │

. │ │ │ │

n │ │ │ │

────┼──────────────┼──────────────┼────────────┼──────────────────

│ n │ n 2 │ │ n 2

│SUM дельта x =│SUM дельта x =│ │SUM(дельта x + 1)

│i=1 i │i=1 i │ │i=1 i

В каждой строчке вычисляют значения , , , складывают результаты вычислений по каждой графе и проверяют их правильность тождеством.

Характеристики и вычисляют по формулам (1) и (2), подставляя в них подсчитанные по табл. 2 значения и .

3. Для расчета характеристик точности в объединенной выборке и проверки согласия действительного распределения с теоретическим действительные отклонения из всех выборок малого объема выписывают в порядке их возрастания, и полученное поле рассеяния между наименьшим и наибольшим отклонениями разбивают на интервалы распределения, равные цене деления измерительного инструмента, принимая целые числа за середины интервалов (= 1, 2, 3, ..., - количество интервалов).

4. Подсчитывают количество отклонений, относящихся к каждому интервалу (частоты ), и по форме табл. 3 (левая часть) строят гистограмму действительных отклонений, откладывая по вертикали интервалы распределения, а по горизонтали - соответствующие им частоты.

Таблица 3

Форма таблицы для построения гистограммы

и расчета характеристик и в объединенной выборке

─────────────┬──────────────────────────────────┬───────┬─────────┬────────────┬───────────────┬────────────────┬────────────────┬─────────────────────

Центры интер-│Частота отклонений в интервалах f │ f │ 2│ │ 2│ │ 2 │ 2

валов распре-│ j│ j │дельта x │дельта x + 1│(дельта x + 1) │ f дельта x │f дельта x │ f (дельта x + 1)

деления ├─┬─┬─┬─┬─┬─┬─┬─┬─┬──┬──┬──┬───────┤ │ j│ j │ j │ j j │ j j │ j j

дельта х │1│2│3│4│5│6│7│8│9│10│11│12│ ... │ │ │ │ │ │ │

j │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │ │

─────────────┼─┴─┴─┴─┴─┴─┴─┴─┴─┴──┴──┴──┴───────┼───────┼─────────┼────────────┼───────────────┼────────────────┼────────────────┼─────────────────────

1 │ 2 │ 3 │ 4 │ 5 │ 6 │ 7 │ 8 │ 9

─────────────┼──────────────────────────────────┼───────┼─────────┼────────────┼───────────────┼────────────────┼────────────────┼─────────────────────

дельта x │ │ │ │ │ │ │ │

jmax │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

... │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

+ 1 │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

0 │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

- 1 │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

... │ │ │ │ │ │ │ │

─────────────┤ │ │ │ │ │ │ │

дельта x │ │ │ │ │ │ │ │

jmin │ │ │ │ │ │ │ │

─────────────┴──────────────────────────────────┼───────┼─────────┼────────────┼───────────────┼────────────────┼────────────────┼─────────────────────

│ m │ │ │ │ m │ m 2 │ m 2

│SUM f =│ - │ - │ - │SUM f дельта x =│SUM f дельта x =│SUM f (дельта x + 1)

│j=1 j │ │ │ │j=1 j j │j=1 j j │j=1 j j

При построении гистограммы следует учитывать, что отклонения конфигурации элементов всегда имеют положительный знак.

В правую часть табл. 3 заносят значения , , , , , вычисленные для каждого значения , принятого за середину интервала, и проверяют правильность вычислений тождеством

Значения и вычисляют по преобразованным формулам (1) и (2):

, (1а)

, (2а)

подставляя в них соответствующие суммы чисел из таблицы.

После вычисления и действительные отклонения , выходящие за пределы интервалов, в которые попадают значения , исключают из гистограммы и табл. 3 как грубые ошибки, после чего уточняют значения и .

5. На полученной гистограмме по характеристикам и строят кривую нормального распределения. С этой целью в соответствии с табл. 4 вычисляют значения и частоты , соответствующие нормальному распределению, и, отложив эти значения на вертикальной и горизонтальной шкале левой части табл. 3, по полученным на гистограмме точкам с координатами и строят плавную кривую.

Таблица 4

──────┬─────────┬───────────────┬────────────────┬────────────────

│ │ │ │

дельта│дельта x │дельта x +/- S │дельта x +/- 2S │дельта x +/- 3S

│ m│ m x│ m x│ m x

──────┼─────────┼───────────────┼────────────────┼────────────────

f │ f │ 5 │ 1 │ 1

│ max │ - f │ - f │ --- f

│ │ 8 max │ 8 max │ 80 max

│ │ │ │

Значение определяют по формуле

а для отклонений конфигурации - по формуле

6. При отсутствии на гистограмме резких отличий от построенной кривой (пиков распределения у ее границ, явно выраженных нескольких вершин и т.п.), по интервалам распределения, расположенным за пределами при 2; 2,4 и 3 определяют сумму частностей действительных отклонений в процентах по формуле

где - число интервалов за пределами .

Распределение считают приближающимся к нормальному, если найденные суммы частностей не превышают соответствующих значений, приведенных в табл. 5.

Таблица 5

───────────────┬─────────────────┬───────────────┬────────────────

t │ 2,0 │ 2,4 │ 3,0

───────────────┼─────────────────┼───────────────┼────────────────

SUM W , % │ 12,5 │ 8,6 │ 5,55

j │ │ │

7. Стабильность выборочного среднего отклонения и размахов в серии мгновенных выборок проверяют условиями:

где и - коэффициенты, принимаемые по табл. 6 в зависимости от объема мгновенных выборок n.

Таблица 6

────────────────┬───────────────────────┬─────────────────────────

n │ A │ A

│ 1 │ 2

────────────────┼───────────────────────┼─────────────────────────

5 │ 1,34 │ 4,89

6 │ 1,22 │ 5,04

7 │ 1,13 │ 5,16

8 │ 1,06 │ 5,25

9 │ 1,00 │ 5,34

10 │ 0,95 │ 5,43

При устойчивом технологическом процессе не менее 95% значений и должны соответствовать указанным условиям.

8. Стабильность характеристик и в серии выборок объемом проверяется вычислением показателей и по формулам:

где и - соответственно наибольшее и наименьшее значения характеристики в серии выборок;

и - значения характеристики в выборках с характеристиками и .

Характеристики и в серии выборок считаются стабильными, если , .

1 - 8. (Измененная редакция, Изм. N 1).

Приложение 2

Справочное

ПРИМЕР

ПРОВЕРКИ СТАТИСТИЧЕСКОЙ ОДНОРОДНОСТИ

ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА

Необходимо произвести проверку статистической однородности технологического процесса изготовления панелей наружных стен. Анализируемый параметр - длина. Номинальные длины всех марок панелей находятся в интервале от 2500 до 4000 мм. Панели изготавливаются в горизонтальных формах, объем выпуска - 25 панелей в смену. Парк форм для изготовления панелей - 96 шт., каждая из которых имеет свои действительные внутренние размеры, влияющие на точность соответствующих размеров панелей. Подобный технологический процесс относится к процессам серийного производства.

1. Для составления выборки объемом изделий ежедневно в течение трех дней записывались действительные отклонения длины панелей, которые контролировались в соответствии с ГОСТ 11024-84 (по 5 изделий в каждую смену). Из накопленных 45 действительных отклонений были исключены пять отклонений длины изделий из форм, которые попали в контроль повторно.

Результаты измерений были округлены до целых значений в мм и занесены в табл. 1, составленную по форме табл. 2 Приложения 1, после чего в табл. 1 были выполнены необходимые вычисления.

Таблица 1

───┬─────────────────┬──────────────────┬─────────────────┬───────────────────────

N │ дельта x │ 2 │ │ 2

п/п│ i │ дельта x │ дельта x + 1 │ (дельта x + 1)

│ │ i │ i │ i

───┼─────────────────┼──────────────────┼─────────────────┼───────────────────────

1 │ 2 │ 3 │ 4 │ 5

1 │ +4 │ 16 │ +5 │ 25

2 │ -3 │ 9 │ -2 │ 4

3 │ -1 │ 1 │ 0 │ 0

4 │ +2 │ 4 │ +3 │ 9

5 │ -1 │ 1 │ 0 │ 0

6 │ 0 │ 0 │ +1 │ 1

7 │ -4 │ 16 │ -3 │ 9

8 │ -1 │ 1 │ 0 │ 0

9 │ +2 │ 4 │ +3 │ 9

10 │ +1 │ 1 │ +2 │ 4

11 │ +4 │ 16 │ +5 │ 25

12 │ +1 │ 1 │ +2 │ 4

13 │ +1 │ 1 │ +2 │ 4

14 │ +3 │ 9 │ +4 │ 16

15 │ +2 │ 4 │ +3 │ 9

16 │ 0 │ 0 │ +1 │ 1

17 │ +5 │ 25 │ +6 │ 36

18 │ +3 │ 9 │ +4 │ 16

19 │ +1 │ 1 │ +2 │ 4

20 │ +2 │ 4 │ +3 │ 9

21 │ +6 │ 36 │ +7 │ 49

22 │ +2 │ 4 │ +3 │ 9

23 │ +2 │ 1 │ +2 │ 4

24 │ +7 │ 49 │ +8 │ 64

25 │ +3 │ 9 │ +4 │ 16

26 │ +2 │ 4 │ +3 │ 9

27 │ +1 │ 1 │ +2 │ 4

28 │ 0 │ 0 │ +1 │ 1

29 │ +3 │ 9 │ +4 │ 16

30 │ +2 │ 4 │ +3 │ 9

31 │ 0 │ 0 │ +1 │ 1

32 │ +5 │ 25 │ +6 │ 36

33 │ +6 │ 36 │ +7 │ 49

34 │ +2 │ 4 │ +3 │ 9

35 │ +1 │ 1 │ +2 │ 4

36 │ -3 │ 9 │ -2 │ 4

37 │ +2 │ 4 │ +3 │ 9

38 │ +3 │ 9 │ +4 │ 16

39 │ +4 │ 16 │ +5 │ 25

40 │ -5 │ 25 │ -4 │ 16

├─────────────────┼──────────────────┼────────────┬────┼───────────────────────

│40 │40 2 │ │ │40 2

│SUM дельта x = 63│SUM дельта x = 369│дельта x + 1│ │SUM(дельта x + 1) = 535

│ 1 i │ 1 i │ i │ │ 1 i

Правильность заполнения таблицы в соответствии с п. 1 Приложения 1 была проверена тождеством

535 = 369 + 263 + 40,

после чего по формулам (1) и (2) определены

мм;

мм.

2. В течение последующих пяти месяцев в аналогичном порядке были образованы еще пять выборок того же объема , для каждой из которых были вычислены те же статистические характеристики и .

Сроки отбора выборок устанавливались таким образом, чтобы время между соседними выборками было больше, чем время формирования выборки.

Результаты вычислений статистических характеристик по всем выборкам приведены в табл. 2.

Таблица 2

───────┬────────────────┬────┬────────────────────┬───────────────

N п\п │ Месяц, год │ n │ дельта x , мм │ S , мм

│ │ │ m │ x

───────┼────────────────┼────┼────────────────────┼───────────────

1 │ 05.78 │ 40 │ 1,57 │ 2,60

2 │ 06.78 │ 40 │ 1,43 │ 2,13

3 │ 07.78 │ 40 │ 0,92 │ 2,22

4 │ 08.78 │ 40 │ 1,05 │ 2,35

5 │ 09.78 │ 40 │ 1,36 │ 2,18

6 │ 10.78 │ 40 │ 0,87 │ 2,57

3. Из действительных отклонений во всех выборках были выбраны наибольшее мм и наименьшее мм значения и поле рассеяния между ними разделено на 18 интервалов по 1 мм с границами, равными 10,5; 9,5; 8,5; 7,5 мм и т.д. Центры интервалов, выраженные целыми числами ( 10, 9, 8, 7 мм и т.д.), были занесены в графу 2 табл. 3.

Действительные отклонения из всех выборок были распределены по интервалам, после чего было подсчитано количество отклонений в каждом интервале (частоты), построена гистограмма и выполнены все промежуточные вычисления в таблице. Правильность заполнения таблицы в соответствии с п. 4 Приложения 1 была проверена тождеством

;

2777 = 1935 + 2301 + 240

Характеристики и были вычислены по формулам (1а) и (2а) рекомендуемого Приложения 1:

мм;

мм.

Далее вычислены значения

мм;

мм.

Отклонения, вышедшие за пределы, ограниченные вычисленными значениями и равные +10 мм, +9 мм и -7 мм, были исключены из объединенной выборки, как грубые ошибки, после чего в двух последних графах табл. 3 были произведены соответствующие вычисления, определены новые значения сумм и и уточнены характеристики

мм;

мм.

4. Для построения на чертеже гистограммы кривой нормального распределения в соответствии с п. 4 Приложения 1 были вычислены координаты точек кривой - отклонения и соответствующие им частоты .

──────────────────────────────┬───────────────────────────────────

│ 237

│ f = f = -------------- = 39,5

дельта = дельта x = 1,2 мм │ 1 max ________

1 m │ 2,2 \/ 2 пи

│

──────────────────────────────┼───────────────────────────────────

дельта = дельта x + S = │

2 m x │

│

= 1,2 + 2,4 = 3,6 мм │ 5

│ f = - f = 24,68

│ 2,3 8 max

дельта = дельта x - S = │

3 m x │

│

= 1,2 - 2,4 = -1,2 мм │

──────────────────────────────┼───────────────────────────────────

дельта = дельта x + 2S = │

4 m x │

│

= 1,2 + 4,8 = 6,0 мм │ 1

│ f = - f = 4,93

│ 4,5 8 max

дельта = дельта x - 2S = │

5 m x │

│

= 1,2 - 4,8 = -3,6 мм │

──────────────────────────────┼───────────────────────────────────

дельта = дельта x + 3S = │

6 m x │

│

= 1,2 + 7,2 = 8,4 мм │ 1

│ f = -- f = 0,49

│ 6,7 80 max

дельта = дельта x - 3S = │

7 m x │

│

= 1,2 - 7,2 = -6,0 мм │

Таблица 3

Гистограмма действительных отклонений

и таблица расчета статистических характеристик

По полученным координатам и на гистограмме были найдены характерные точки, по которым была построена теоретическая кривая нормального распределения.

Очертания гистограммы практически можно считать совпадающими с кривой нормального распределения.

Для завершения проверки по гистограмме были суммированы частоты по интервалам, расположенным за границами при 2,0; 2,4; 3,0, и определены соответствующие им суммы частностей.

Сравнение сумм частностей в табл. 4 с допустимыми значениями в табл. 5 Приложения 1 показывает, что исследуемое распределение можно считать приближающимся к нормальному.

Таблица 4

─────────────────┬────────────┬──────────────────────┬────────────

Границы │Сумма частот│ Сумма частностей │Допустимые

│ │ │суммы част-

дельта x +/- tS │ m │ m │ностей по

m x│ t │ t │табл. 5

│ SUM f │ m SUM f │Приложения 1

│ j=1 j │ t j=1 j │

│за границами│SUM W = ------ х 100%│

│ │j=1 j n │

│ │ │

─────────────────┼────────────┼──────────────────────┼────────────

│ │ 3 │

t = 3,0; │ 3 │ --- х 100 = 1,2658 │ 5,55

1,2 +/- 7,2 мм │ │ 240 │

│ │ │

│ │ 8 │

t = 2,4; │ 8 │ --- х 100 = 3,3755 │ 8,60

1,2 +/- 5,8 мм │ │ 240 │

│ │ │

│ │ 19 │

t = 2,0; │ 19 │ --- х 100 = 8,0168 │ 12,50

1,2 +/- 4,8 мм │ │ 240 │

5. Для проверки стабильности характеристики из табл. 2 были выбраны наибольшее и наименьшее значения мм и мм и вычислена характеристика

Характеристика в серии выборок стабильна, так как 1,49 < 1,50 (см. п. 8 Приложения 1).

Для проверки стабильности характеристики из табл. 2 были выбраны наибольшее и наименьшее значения мм и мм, соответствующие им значения мм и , и вычислена характеристика

Характеристика в серии выборок стабильна, так как 1,26 < 2 (см. п. 8 Приложения 1).

6. На основании проверки технологический процесс изготовления панелей наружных стен по параметру "длина панелей" можно считать статистически однородным.

Так как систематическая погрешность, равная найденному выборочному среднему отклонению мм, превышает значение мм, то в соответствии с п. 4.7 настоящего стандарта она должна быть устранена регулированием внутренних размеров форм.

7. Для определения класса точности по длине панелей, в соответствии с п. 5.2 настоящего стандарта определяем значение

мм.

Значение принято по таблице п. 5.2 настоящего стандарта для приемочного уровня дефектности , выбранного по ГОСТ 23616-79.

В соответствии с табл. 1 ГОСТ 21779-82 ближайшее большее значение допуска для интервала номинальных размеров от 2500 до 4000 мм равняется 10 мм, что соответствует 5-му классу точности.

По формуле (5) настоящего стандарта вычисляем значение

В соответствии с п. 5.4 настоящего стандарта можно сделать вывод, что запас точности отсутствует, так как 0,01 < 0,14.

1 - 7. (Измененная редакция, Изм. N 1).